El VaR estima la pérdida máxima de un activo financiero que se puede producir en un escenario adverso, con una cierta probabilidad y durante un horizonte temporal dado. El VaR contempla solo el riesgo de pérdida, el riesgo genuino, mientras que la volatilidad abarca la dispersión en torno a la media, tanto favorable como desfavorable.
El riesgo de ganar no existe
El método Value at Risk (VaR) busca conclusiones del tipo la pérdida máxima durante los próximos n días será de X euros con un nivel de confianza del y%. Ello exige definir el plazo y el nivel de confianza para obtener la pérdida máxima esperada. Este riesgo expresa que, para un plazo, por ejemplo, de 10 días y un nivel de confianza del 95% la probabilidad de perder como máximo 100.000 € en los próximos 10 días es el 95%. En cinco días de cada 100 la pérdida podría superar los 100.000 euros.
El VaR mide solo el riesgo de perder
Si el resultado sigue la distribución normal de la campana de Gauss, la figura muestra el VaR. La parte izquierda de la campana representa el ejemplo anterior. Si el área bajo la campana representa el cien por cien de la probabilidad, el área correspondiente al 95% del nivel de confianza, a la izquierda de la línea corta vertical, mide ese 5% de probabilidad de perder más de 100.000 euros.
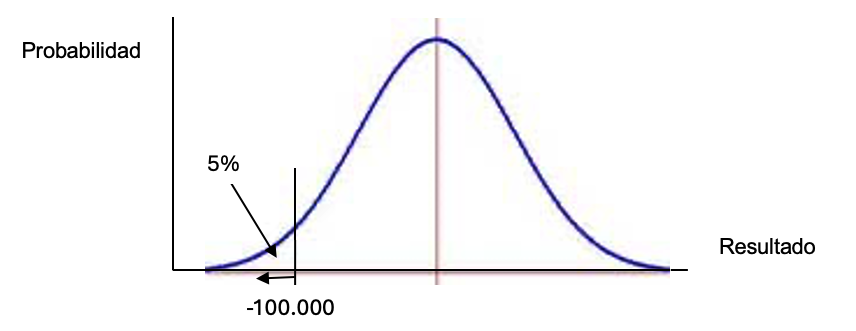
El método para estimar el Value at Risk
El cálculo del VaR considera que la distribución del resultado cuyo riesgo se mide se distribuye normalmente, definida por su media y su desviación típica.
Un tesorero estima a partir de los datos históricos ajustados a la coyuntura, que las ventas del próximo mes se comportarán como una distribución normal con un valor medio de 10,2 millones de euros y una desviación típica de 0,6 millones. Si desea calcular el VaR de esa facturación con un 95% de confianza, el límite inferior en la distribución normal se produce con -1,65 veces la desviación típica. Esto significa que hay una probabilidad del 5% de que las ventas sean inferiores a 1,65 desviaciones típicas. Por lo tanto:
VaR (al 95% de confianza) = 10,2 – 1,65 x 0,6 = 9,21 millones
Esto implica que con un nivel de confianza del 95% que las ventas superarán los 9,21 millones. Una información valiosa para presupuestar el beneficio o la tesorería. Para otros niveles de confianza usados habitualmente solo cambia el estadístico:
VaR (al 90% de confianza) = 10,2 – 1,28 x 0,6 = 9,432 millones
VaR (al 99% de confianza) = 10,2 – 2,33 x 0,6 = 8,802 millones
¿Quieres especializarte en dirección financiera? Estudia el Máster de Converthia
Control de la pérdida máxima de una posición larga de $100.000
Supongamos que la desviación típica de la cotización del dólar es del 0,885% al día sobre la media, correspondiendo a una volatilidad anual del 14%. El VaR de un día se extrapola para cualquier período multiplicando por la raíz cuadrada del número de días del período. Con 250 días de mercado:
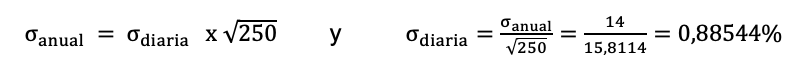
Si se establece un nivel de confianza del 99% (estadístico de 2,33) el resultado es:
Desviación típica diaria = 0,0088544 x 100.000 = 885,44 dólares
VaR (al 99% de confianza) = 2,33 x 885,44 = 2.063,07 dólares
Si se desea calcular la pérdida máxima en los próximos 10 días, se aplica:
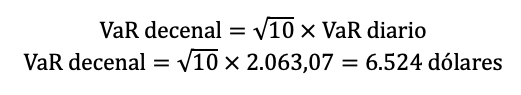
De estas fórmulas se deduce la ecuación genérica para hallar el VaR de t días:
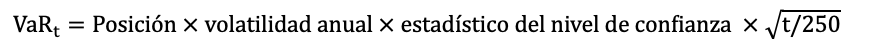
Para el ejemplo anterior se comprueba que:
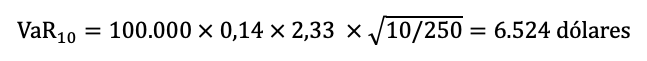
Máster en Control de Gestión
Control de la pérdida máxima de una cartera de 1.000.000 €
Si la desviación típica diaria de su valor es del 2,10%, la volatilidad anual es 33,204% (0,021 x 2500,5) y el VaR para un plazo de 30 días con un nivel de confianza del 95% (estadístico de 1,65), aplicando la fórmula anterior, resulta una pérdida máxima de:
VaR30= 1.000.000 x 0,33204 x 1,65 x (30/250)^0,5 =189.786 euros
El Value at risk ayuda a estimar el potencial de pérdida de una exposición a un plazo y con una probabilidad dados. Una buena herramienta para el controller.
Dr. Juan Pérez-Carballo, Socio de Converthia, expertos en finanzas control de gestión





